Trazado de Perspectiva Isométrica

 

Para hacer una perspectiva (imagen 3D) lo más cómodo es hacer previamente una proyección ortogonal (imagen 2D)

Este es un ejemplo de proyección ortogonal con un prisma de base rectangular y una pirámide de base cuadrada.

Para empezar a hacer la perspectiva lo más importante es descifrar las coordenadas de cada punto. Esto se explicará paso a paso en las siguientes imágenes…

¿Cómo dibujo los ejes de la perspectiva isométrica? Lo primero es dibujar el eje Z, el cual se representa por una línea vertical.

Ahora hay que hacer los dos ejes a 30º. ¿Cómo hacemos eso? Apoyamos la escuadra en la regla “T” tal como se ve en la imagen y a continuación…

Trazamos el eje. En este caso el eje “Y”

Para trazar el eje “X” hacemos el mismo procedimiento.

Los tres ejes “Z; Y; X” respectivamente, se verían así en perspectiva isométrica.

Dibujemos la base del prisma: Para esto tenemos que sacar las coordenadas de la proyección ortogonal. Vamos punto por punto. ¿Dónde está el punto “a” en el eje “x”? Está en el 9, por eso a partir del 9 trazamos una proyectante.

¿Dónde está el punto “a” en el eje “y”? Está en el 6, por eso a partir del 6 trazamos una proyectante.

Y de la intersección de ambas proyectantes surge el punto que estábamos buscando ¡El punto “a”!

Ahora busquemos el punto “b” ¿Dónde está el punto b en el eje “x”? Está en 7, por eso a partir del 7 trazamos una proyectante.

De la intersección de la proyectante que acabamos de hacer, con la proyectante que surge de la otra coordenada (del eje “y”) surge el punto “b”.

¡Ahora busquemos los dos puntos restantes! ¿Dónde está el punto “c” en el eje y? Está en 1, por eso trazamos una proyectante a partir del punto 1. Y dado que el punto d, tiene su coordenada en el eje “y” también en 1, ¡sin querer ya lo hemos encontrado Listo! Ya encontramos los cuatro puntos que componen la base del prisma.

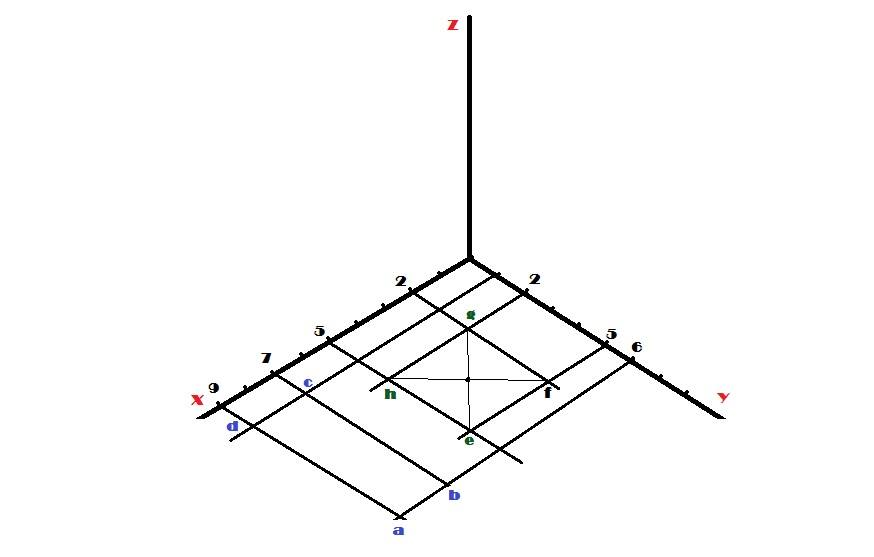
Ahora dibujemos la base de la pirámide: ¿Dónde está el punto “e” en el eje “x”? Está en 3, por eso a partir de él trazamos una proyectante.

¿Donde está el punto “e” en el eje “y”? Está en el punto 5, por eso a partir del 5 trazamos una proyectante. De la intersección de ambas proyectantes surge el punto “e”. Y siguiendo con el mismo procedimiento encontramos los dos puntos faltantes. Sólo debemos preguntarnos ¿Dónde está tal punto en el eje x? ¿Y dónde está ese mismo punto en el eje y?

¡Listo! Ya hemos encontrado las dos bases, tanto la del prisma como la de la pirámide.

¡Sólo falta levantar las alturas! Para construir la altura de la pirámide necesitamos encontrar el punto medio de su base, para esto trazamos “las diagonales”

A partir del punto central de la base (intersección de las diagonales) trazamos verticalmente (paralelo al eje z) la altura. ¿Cuánto debe medir esa altura? Exactamente lo mismo que midió en el PV de la proyección ortogonal.

Ahora sólo resta unir los “vértices”. ¡Acabamos de construir nuestra pirámide de base cuadrada! ♥

Ahora levantemos la altura del prisma. Esto es más fácil. Sencillamente levantamos la altura de los 4 puntos de la base del prisma. Esta altura debe encontrarse de forma absolutamente vertical y debe medir lo mismo en cualquiera de los 4 puntos.

Construidas las alturas del prisma ahora tenemos que unir mediante aristas los vértices encontrados.

¡Listo! Ahora podemos repasar las aristas vistas para divisar mejor lo que acabamos de construir

Ahora (borrando) segmentamos las aristas ocultas, haciendo líneas discontinuas.

¡Fin! Ahora sólo resta pintar teniendo en cuenta los colores que usamos en la proyección ortogonal.

Fuente: https://lamuchachachara.wordpress.com/2016/03/21/perspectiva-isometrica-paso-a-paso/